


Next: Discretization of the TDGL
Up: ON THE NUMERICAL SOLUTION
Previous: Introduction
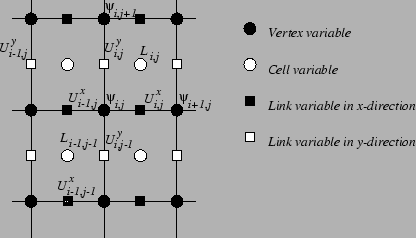
Consider a rectangular mesh such as that of Fig. 1, consisting
of
Nx x Ny cells, with mesh spacings ax and ay.
Any numerical method is defined by the (finite) unknowns of the method plus
the equations relating these unknowns. In the 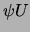 method the
fundamental unknowns are three complex arrays:
method the
fundamental unknowns are three complex arrays:
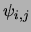 ,
with
,
with
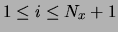 ,
,
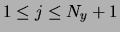 ,
associated to the nodes (or vertices) of the
mesh. The value of
,
associated to the nodes (or vertices) of the
mesh. The value of 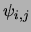 approximates that of the order
parameter at position (xi,yj). In the program, the
corresponding array is F(i,j).
approximates that of the order
parameter at position (xi,yj). In the program, the
corresponding array is F(i,j).
- Uxi,j (link variable in the x-direction,
with
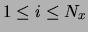 ,
,
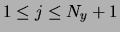 ,
associated to the horizontal links (cell edges) of the mesh. The
value Uxi,j approximates that of
,
associated to the horizontal links (cell edges) of the mesh. The
value Uxi,j approximates that of
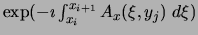 .
.
- Uyi,j (link variable in the y-direction,
with
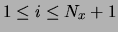 ,
,
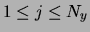 ,
associated to the vertical links of the mesh. The
value Uyi,j approximates that of
,
associated to the vertical links of the mesh. The
value Uyi,j approximates that of
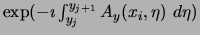 .
.
To derive the discrete equations it is useful to notice that, from the
definition of the link variables, discrete analogs of 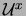 and
and 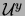 from (1)-(2) can be defined at the
nodes as
from (1)-(2) can be defined at the
nodes as
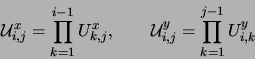 |
(8) |
which leads to
 |
(9) |
Figure 1:
Scheme of computational cells defining the numbering of
discrete variables.
|



Next: Discretization of the TDGL
Up: ON THE NUMERICAL SOLUTION
Previous: Introduction
Gustavo Carlos Buscaglia
2000-07-20
![]() method the
fundamental unknowns are three complex arrays:
method the
fundamental unknowns are three complex arrays: