


Next: Numerical method
Up: ON THE NUMERICAL SOLUTION
Previous: ON THE NUMERICAL SOLUTION
The numerical simulation of superconductivity has attracted increasing
attention during the last years, specially due to the appearance of
high-temperature superconductors. At the mesoscopic level, the governing
equations are provided by the Ginzburg-Landau theory, and are frequently
referred to as TDGL equations (for Time Dependent Ginzburg-Landau
equations). These are coupled nonlinear partial differential equations for
the (complex) order parameter 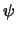 and for the electromagnetic vector
potential
and for the electromagnetic vector
potential 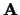 (the scalar potential is usually eliminated through an
appropriate choice of gauge).
(the scalar potential is usually eliminated through an
appropriate choice of gauge).
Numerical approximations to the TDGL equations
have been derived using both finite element [1] and finite difference
[2,3,4,5,6,7] methods. Most physical
applications use a specific finite difference method that we will refer to
as 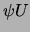 -method. The unknowns in the
-method. The unknowns in the 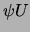 -method in two spatial
dimensions are the order parameter
-method in two spatial
dimensions are the order parameter 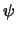 and two auxiliary fields,
and two auxiliary fields,
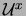 and
and 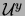 ,
that are related to
,
that are related to 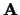 by
by
The point (xo, yo) is arbitrary,
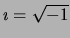 .
Such variables were first
introduced in lattice gauge theories [8]. To our knowledge they were
first applied to the TDGL equations by Liu et al [3]. The
.
Such variables were first
introduced in lattice gauge theories [8]. To our knowledge they were
first applied to the TDGL equations by Liu et al [3]. The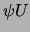 -method has since proved useful in the numerical simulation of many
superconductivity phenomena [3,5,6,7].
-method has since proved useful in the numerical simulation of many
superconductivity phenomena [3,5,6,7].
The TDGL equations coupled with Maxwell equations with the zero-scalar potential
gauge choice lead to the following mathematical problem:
where lengths have been scaled in units of 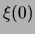 ,
time in units of
,
time in units of
 ,
,
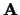 in units of
in units of
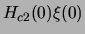 and
temperatures in units of Tc.
It has been assumed that the coherence
length
and
temperatures in units of Tc.
It has been assumed that the coherence
length 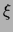 obeys
obeys
 ,
where T is the
temperature in units of the critical temperature Tc,
and that the Ginzburg-Landau
parameter
,
where T is the
temperature in units of the critical temperature Tc,
and that the Ginzburg-Landau
parameter 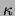 is independent of temperature.
is independent of temperature.
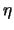 is a positive
constant (a ratio of characteristic times for
is a positive
constant (a ratio of characteristic times for 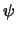 and
and 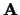 ),
),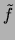 a random force simulating thermal fluctuations, kB the
Boltzmann constant and Hc2 the upper critical magnetic field for
type-II superconductors (see [9]).
a random force simulating thermal fluctuations, kB the
Boltzmann constant and Hc2 the upper critical magnetic field for
type-II superconductors (see [9]). 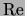 stands for ``real part
of''.
stands for ``real part
of''.
Eqs. (3)-(4) are to be solved in a bounded domain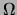 ,
complemented with initial conditions for
,
complemented with initial conditions for 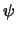 and
and 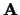 ,
together with the following boundary conditions:
,
together with the following boundary conditions:
- - Boundary condition for
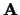 :
:
- A given applied magnetic
field He in the z-direction, possibly time-dependent but
spatially uniform, is assumed.
Continuity of the field thus implies
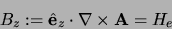 |
(5) |
- - Boundary condition for
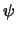 :
:
- Zero supercurrent density perpendicular to the
boundary is imposed, namely,
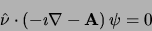 |
(6) |
where 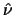 denotes the unit normal to the superconductor-vacuum
interface. This automatically implies that the normal current
perpendicular to the boundary also vanishes, since the total
current across the superconductor-vacuum interface is zero.
To see this, let
denotes the unit normal to the superconductor-vacuum
interface. This automatically implies that the normal current
perpendicular to the boundary also vanishes, since the total
current across the superconductor-vacuum interface is zero.
To see this, let
![${\bf J}_s=(1-T) {\rm Re} [{\overline \psi}
\left( -\imath\nabla -{\bf A}\right) \psi] $](img29.png) denote the supercurrent
density and
denote the supercurrent
density and
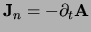 the normal current
density. Rewrite Eq. 4 as
the normal current
density. Rewrite Eq. 4 as
Projection of this equation along the normal
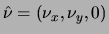 leads to
leads to
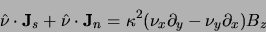 |
(7) |
Since
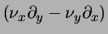 is nothing but the tangential
derivative, and considering that the applied field He is uniform,
the right-hand side of (7) identically vanishes showing that
the total current across the boundary is zero.
is nothing but the tangential
derivative, and considering that the applied field He is uniform,
the right-hand side of (7) identically vanishes showing that
the total current across the boundary is zero.
For later use, we define the magnetization Mz as (see, e.g., [9])



Next: Numerical method
Up: ON THE NUMERICAL SOLUTION
Previous: ON THE NUMERICAL SOLUTION
Gustavo Carlos Buscaglia
2000-07-20
![]() and for the electromagnetic vector
potential
and for the electromagnetic vector
potential ![]() (the scalar potential is usually eliminated through an
appropriate choice of gauge).
(the scalar potential is usually eliminated through an
appropriate choice of gauge).
![]() -method. The unknowns in the
-method. The unknowns in the ![]() -method in two spatial
dimensions are the order parameter
-method in two spatial
dimensions are the order parameter ![]() and two auxiliary fields,
and two auxiliary fields,
![]() and
and ![]() ,
that are related to
,
that are related to ![]() by
by
![]() ,
complemented with initial conditions for
,
complemented with initial conditions for ![]() and
and ![]() ,
together with the following boundary conditions:
,
together with the following boundary conditions: