If the boundary is aligned with the y-axis, the
zero-current condition implies
![]() or, equivalently,
or, equivalently,
![]() .
For the order parameter at i=1 (West boundary) and i=Nx+1 (East boundary)
this is implemented as
.
For the order parameter at i=1 (West boundary) and i=Nx+1 (East boundary)
this is implemented as
For the link variables, it remains to define how to update the values of
those on the boundary. Notice that,
for cells with two edges on
the boundary only the product of the two link variables has
numerical consequences, since it is the total circulation of
the vector potential around the cell that propagates inside the
computational domain. We have thus one unknown for each cell
on the boundary, with the other
three link variables already calculated from Eq. (19)
or Eq. (20). Let He be the applied field and let
the cell (i,j) be at the boundary. From
Remark: Notice that it is not difficult to obtain second
order approximations to the boundary conditions that would preserve
the accuracy of the scheme of Eqs. (18)-(20).
Taking as example the East boundary (i=Nx+1), a second order
approximation of the zero-current condition leads to
| = | 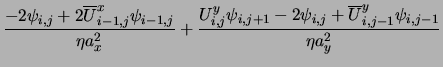 |
||
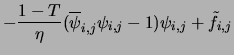 |
(25) |