If the domain is multiply connected, at the hole boundary the same boundary conditions as before apply, namely zero perpendicular supercurrent and magnetic field continuity. In what concerns the order parameter, one proceeds exactly as for the exterior boundary (Eqs. (22) and (23)). However, the magnetic field inside the hole is not known a priori. Our methodology has been implemented for the case of one rectangular hole, but it is easily generalized. Let Hi be the magnetic field inside the hole. Since there are no currents in the hole, Hi is uniform and only depends on time.
Consider the hole shown in Fig. 2. It is delimited
by the vertex lines i=W, i=E, j=S and j=N. Since the
adjacent cells must also have Bz=Hi, the magnetic field
is uniform in the subdomain ![]() depicted in Fig. 2.
The key remark is that the link variables corresponding to
the boundary of
depicted in Fig. 2.
The key remark is that the link variables corresponding to
the boundary of ![]() can be calculated using Eqs. (19)
and (20).
can be calculated using Eqs. (19)
and (20).
The algorithm to update Hi and the link variables at the boundary of the hole is (with a notation similar to that in the program):
| = | 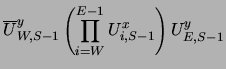 |
(26) | |
| = | 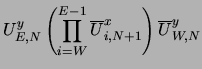 |
(27) | |
| = | 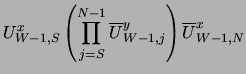 |
(28) | |
| = | 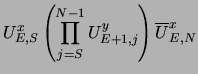 |
(29) |
| (30) |
The implementation uses the logical array Bulk (i,j) to determine if cell (i,j) is in the superconductor or in the hole.