TDGL: Time dependent Ginzburg-Landau solver
Fortran program, uses finite difference method based
on gauge-invariant link variables. Reference: "On
the numerical solution of the time-dependent Ginzburg-Landau equations
in multiply connected domains", G. Buscaglia, C. Bolech and A. López,
to appear in Connectivity&Superconductivity, J. Berger and J. Rubinstein
(Eds.), Springer.
Here you can download
It should compile without trouble. The data file corresponds
to a small case (case III in the reference), with 64x64 cells and 250,000
time steps. This case takes about thirty minutes to run on my PC (750 MHz).
You will get two output files, c.dat and s.dat, of summary results. Most
detailed is s.dat, of which the first column is the time-step number, the
second the applied field, the third the internal field (inside the hole),
the fourth the total average field (B), the fifth the magnetization, the
sixth the free energy, the following two the number of fluxoids inside
different paths and the last two the minimum values of the modulus of the
order parameter along the same paths. By reading the program and the associated
paper the meaning of these results should be evident. You will also get
several graphic files (*.gra) containing the values of the modulus of the
order parameter for each cell in the mesh, that you should be able to visualize
with an appropriate package, and finally several restart files (*.ree).
In case you wanted to reccommence a calculation from one of these restart
files, all you must do is rename it as "tdgl.ree".
I'm sorry for the names of the graphics and restart
files, I'm sure it can be done much better.
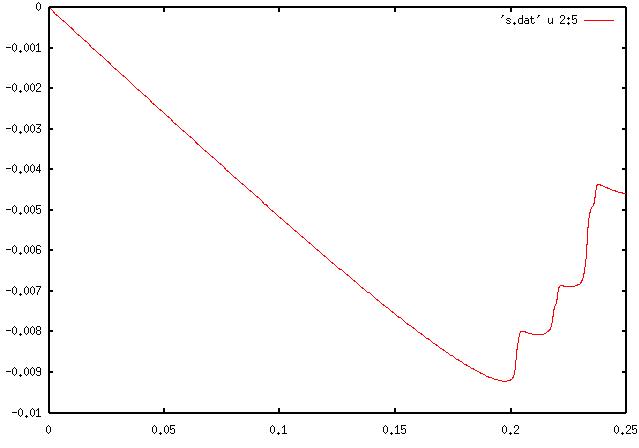
Anyway, just for testing, once you have run the
code, if you plot the fifth column of s.dat as a function of the second
column, you should find a nice magnetization curve as the following:
Best wishes,
Gustavo C. Buscaglia, 20 July 2000

